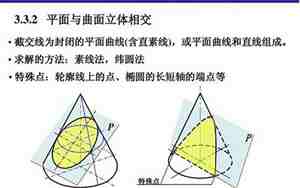
曲面和平面相交线的关系

曲面和平面相交线，平面与曲面相交成什么线。

曲面和平面是几何学中非常基本的概念，它们之间的相互作用在我们的日常生活中随处可见。当曲面和平面相交时，会产生一个交线。而当平面与曲面相交时，会产生一个曲线。本文将探讨这些相交线和相交曲线的性质和应用。

1. 曲面和平面相交线。

曲面和平面相交产生的交线，常称为曲面的截线或平面的截痕。它是曲面和平面的交集，是一个线段或线段的组合。通常我们用数学语言来描述截线，即用方程组来表示曲面和平面的交点。

对于曲面，我们可以用一个方程组来表示它的形状。比如，一个二次曲面的方程可以表示为：。

ax^2 + by^2 + cz^2 + dxy + exz + fyz + gx + hy + iz + j = 0。

对于平面，我们可以用一个点和一个向量来表示它的位置和方向。比如，平面的方程可以表示为：。

(Ax + By + Cz + D) = 0。

其中，A,B,C是该平面的法向量，D是该平面到坐标原点的距离。

当我们将平面的方程代入曲面的方程组中，可以求出它们交点的坐标。这个坐标可以用来确定曲面和平面相交线的位置和长度。

2. 平面与曲面相交曲线。

平面和曲面之间的相互作用，也可以产生一些非常有趣的几何形状。当平面与曲面相交时，会产生一个曲线。这个曲线通常被称为曲面的切线或平面的割线。

与曲面截线不同的是，平面割线是一个曲线，而不是一个线段。它的形状可以是任意形状，包括圆形、椭圆形、抛物线、双曲线等等。这些形状取决于曲面和平面的相对位置和方向。

对于一个平面，我们可以用一个点和一个向量来描述它的位置和方向。对于一个曲面，我们可以用一个方程来描述它的形状。当我们把平面的方程代入曲面的方程中，可以求出它们相交的点。这些点连成的曲线，就是平面与曲面相交的割线。

3. 总结。

曲面和平面是几何学中非常基本的概念，它们之间的相互作用产生了许多有趣的几何形状。当曲面和平面相交时，会产生曲面的截线或平面的截痕。这些截线可以用数学方程来描述它们的位置和长度。当平面与曲面相交时，会产生曲面的切线或平面的割线。这些割线的形状可以是任意形状，取决于曲面和平面的相对位置和方向。在实际应用中，曲面和平面的交线和相交曲线可以用来计算几何形状、模拟物理过程、进行工程设计等等。

平面与曲面相交.

当一个平面和一个曲面相交时，它们通常会形成一条曲线或者曲面上的一条曲线。这条曲线可以是一个圆、椭圆、抛物线、双曲线等等。在某些情况下，相交线还可以是一条直线。当一个曲面和一个平面相交时，相交线的形状也会与上述相似。不同的是，相交线的位置通常更容易确定，因为平面相对于曲面来说非常简单，容易掌握。相交线的形状也可以通过求解两个方程的交点来计算得到。

曲面与平面的交线怎么求

曲面和平面相交线的求法如下：。1. 设曲面的方程为 F(x,y,z) = 0，平面的方程为 Ax + By + Cz + D = 0。2. 解出其中一个变量，例如令 z = g(x,y)，则有 F(x,y,g(x,y)) = 0。3. 将 z = g(x,y) 代入平面方程，得到 Ax + By + Cg(x,y) + D = 0。4. 解出另一个变量，例如令 y = h(x)，则有 Ax + B h(x) + C g(x,h(x)) + D = 0。5. 将 y = h(x) 代入 F(x,y,g(x,y)) = 0，得到只含有 x 的方程，解出 x。6. 将得到的 x 带入 y = h(x) 和 z = g(x,y)，即可得到相交线的参数方程。需要注意的是，如果曲面和平面相交的情况比较复杂，可以尝试使用数值计算或者图形化分析的方法来求解。

是直线和曲线吗

是的，曲面和平面的相交线可能是直线，也可能是曲线。这取决于它们的具体交点和曲面的形状。

平面与曲面交线怎么求

曲面和平面相交线的求解：。1. 将曲面和平面的方程联立，得到一个方程组。2. 消去其中一个未知数，得到一个方程，表示相交线的参数式或一般式。3. 如果需要，再进一步转化为点向式或斜截式。平面与曲面交线的求解：。1. 将曲面的方程代入平面的方程，得到一个一元二次方程。2. 求解该方程，得到参数，代入曲面方程，求出对应的点。3. 如果需要，再进一步转化为点向式或斜截式。

关于二阶曲面与平面相交线为圆的讨论

当一个二阶曲面与平面相交线为圆时，有以下几种情况：。1. 圆与曲面相切：此时曲面有一个特殊点，称为切点。这个点在圆上，并且圆的切线与曲面相切。在这种情况下，曲面可以是一个椭球面、双曲面或抛物面。2. 圆与曲面相离：此时曲面没有交点，但圆的平面与曲面相交。在这种情况下，曲面可以是一个椭球面或双曲面。3. 圆与曲面相交：此时曲面与圆有两个交点，其中一个是切点。在这种情况下，曲面可以是一个椭球面或双曲面。总之，当一个曲面与平面相交线为圆时，它通常是椭球面或双曲面。这是因为圆形相交线需要具有对称性，而只有这两种曲面可以满足这一要求。

一个平面和一个曲面相交得到什麽

对于曲面和平面相交线，通常会得到一个曲线，这个曲线是曲面和平面的交线。在三维空间中，平面和曲面仍然是二维的，因此它们的交线也是二维的，即一个曲线。对于一个平面和一个曲面相交，通常会得到一个曲线或者一个曲面。如果平面只是擦过曲面的一小部分，并没有完全穿透曲面，那么得到的仍然是一个曲线。如果平面完全穿透了曲面，那么得到的就是一个曲面，这个曲面就是曲面和平面的交。