函数拐点怎么求例题及答案

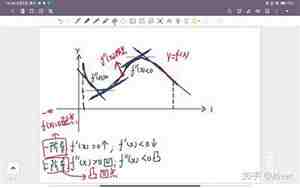
函数的拐点是数学中的一个重要概念，它指的是函数图像上的一个点，在这个点处函数的导数发生了变化，即函数由单调递增变为单调递减，或者由单调递减变为单调递增。对于一个函数来说，找到它的拐点可以帮助我们更好地理解函数的性质和变化趋势。接下来，我们将详细介绍如何求函数的拐点。

首先，我们需要明确一个概念，那就是函数的导数。函数的导数是一个描述函数变化率的概念，它表示函数在某一点上的斜率。在数学中，导数可以通过求函数的极限得到，也可以通过微积分的方法求解。此处我们主要介绍直接求解导数的方法。对于一个函数f(x)，它在某一点x上的导数可以用以下公式表示：。

f'(x) = lim (f(x+h) - f(x))/h (h->0)。

其中h是一个极小的量，表示x的微小变化。这个公式的意义是，当x发生微小变化h时，函数f(x)的变化量除以h就是函数的导数f'(x)。通过这个公式，我们可以求出函数在任意一点上的导数。

接下来，我们来看一下如何求函数的拐点。根据定义，函数的拐点是函数图像上的一个点，在这个点处函数的导数发生了变化。因此，我们可以通过求解函数的导数来确定函数的拐点。具体步骤如下：。

Step 1：求解函数的导数 f'(x)。

Step 2：求解函数的二阶导数 f''(x)。

Step 3：令f''(x)=0，求出x的值。

Step 4：判断f''(x)在x左右两侧的符号，如果f''(x)从负数变为正数，则x是函数的拐点。

具体来说，我们可以将x的值代入函数的二阶导数中，判断f''(x)在x左右两侧的符号。如果f''(x)从负数变为正数，则说明函数的导数从单调递减变为单调递增，也就是函数在该点处的曲率发生了变化，这就是函数的拐点。

举个例子，我们来看一下如何求一个函数的拐点。假设我们要求解函数y=x^3-6x^2+9x+2的拐点。首先，我们要求解函数的一阶导数和二阶导数：。

y'=3x^2-12x+9。

y''=6x-12。

然后，我们令f''(x)=0，求出x的值：。

6x-12=0。

x=2。

接下来，我们判断f''(x)在x=2左右两侧的符号：。

当x<2时，f''(x)<0。

当x>2时，f''(x)>0。

因此，x=2是函数的拐点。

综上所述，求解函数的拐点可以帮助我们更好地理解函数的性质和变化趋势。通过求解函数的导数和二阶导数，我们可以确定函数的拐点，并进一步分析函数的曲率变化。在实际应用中，求解函数的拐点对于优化函数的性能和改进算法效率具有重要意义。

函数拐点的求法

函数的拐点是函数的导数发生变化的点，具体求法如下：。1. 求函数的导数。2. 对导数求导，得到导数的导数，即二阶导数。3. 令二阶导数等于零，解方程得到二阶导数为零的点。4. 判断该点的左右两侧的二阶导数的符号，如果左侧二阶导数为负，右侧二阶导数为正，则该点为函数的拐点。5. 求出拐点的坐标，即将拐点的横坐标代入原函数求出纵坐标。需要注意的是，有些函数可能不存在拐点，或者拐点不唯一。

函数拐点坐标怎么求

函数的拐点可以通过求函数的二阶导数来确定。函数的拐点是指函数在该点处的曲线方向发生了改变，即函数的二阶导数为零。如果函数的二阶导数在某一点处从正数变为负数，则该点为函数的拐点，此时函数从凸向下转变为凸向上；如果函数的二阶导数在某一点处从负数变为正数，则该点为函数的拐点，此时函数从凸向上转变为凸向下。函数拐点坐标可以通过以下步骤求得：。1. 求出函数的二阶导数。2. 解二阶导数为零的方程，求出所有的二阶导数为零的点。3. 对每一个二阶导数为零的点，判断该点的左右两侧的二阶导数符号是否发生了变化，如果是，则该点为函数的拐点。4. 对每个拐点，求出其坐标，即将其代入原函数中求得。注：如果函数存在多个拐点，则需要按照上述步骤逐个求出。

求函数拐点的一般步骤

函数的拐点是指函数图像发生凸凹性变化的点，可以通过求导数来判断。一般步骤如下：。1. 求出函数的一阶导数f’(x)和二阶导数f’’(x)。2. 令f’’(x)=0，解出x的值。3. 判断f’’(x)在x值的左右两侧的符号，如果f’’(x)从正数变为负数，则该点是函数的拐点。4. 根据拐点位置对函数的凸凹性进行判断。拐点左侧为凹函数，右侧为凸函数。5. 检验求解出来的拐点是否为函数图像的奇点，即判断f(x)在该点处是否连续。注意：如果f’’(x)不存在，说明函数在该点处不存在拐点。